Mutation Testing Theory

Mutation Testing is a fault-based testing technique which provides a testing criterion called the "mutation adequacy score". The mutation adequacy score can be used to measure the effectiveness of a test set in terms of its ability to detect faults.

The general principle underlying Mutation Testing work is that the faults used by Mutation Testing represent the mistakes that programmers often make and other related testing heuristics. Such faults are deliberately seeded into the original program, by a simple syntactic change, to create a set of faulty programs called mutants, each containing a different syntactic change. To assess the quality of a given test set, these mutants are executed against the input test set to see if the seeded faults can be detected. The history of Mutation Testing can be traced back to 1971 in a student paper by Richard Lipton [EncyclopediaSE]. The birth of the field can also be identified in other papers published in the late 1970s by DeMillo et al. [DeMilloLS78] and Hamlet [Hamlet77].

Fundamental Hypotheses

Mutation Testing promises to be effective in identifying adequate test data which can be used to find real faults [GeistOH92]. However, the number of such potential faults for a given program is enormous; it is impossible to generate mutants representing all of them. Therefore, traditional Mutation Testing only targets a subset of these faults; those which are close to the correct version of the program with the hope that these will be sufficient to simulate all faults. This theory is based on two hypotheses: the Competent Programmer Hypothesis (CPH) [DeMilloLS78, AcreeBDLS79] and Coupling Effect [DeMilloLS78].

The CPH was first introduced by DeMillo et al. in 1978 [DeMilloLS78]. It states that programmers are competent, which implies that they tend to develop programs close to the correct version. As a result, although there may be faults in the program delivered by a competent programmer, we assume that these faults are merely a few simple faults which can be corrected by a few small syntactical changes. Therefore, in Mutation Testing, only faults constructed from several simple syntactical changes are applied, which represents the faults that are made by "competent programmers". An example of the CPH can be found in Acree et al.'s work [AcreeBDLS79] and a theoretical discussion using the concept of program neighbourhoods can also be found in Budd et al.'s work [BuddDLS80].

The Coupling Effect was also proposed by DeMillo et al. in 1978 [DeMilloLS78]. Unlike the CPH concerning programmer's behaviour, the Coupling Effect concerns the type of faults used in mutation analysis. It states that "Test data that distinguishes all programs differing from a correct one by only simple errors is so sensitive that it also implicitly distinguishes more complex errors". Offutt [Offutt89, Offutt92] extended this into the Coupling Effect Hypothesis and the Mutation Coupling Effect Hypothesis with a precise definition of simple and complex faults (errors). In his definition, a simple fault is represented by a simple mutant which is created by making a single syntactical change, while a complex fault is represented as a complex mutant which is created by making more than one change.

According to Offutt, the Coupling Effect Hypothesis is that "complex faults are coupled to simple faults in such a way that a test data set that detects all simple faults in a program will detect a high percentage of the complex faults" [Offutt92]. The Mutation Coupling Effect Hypothesis now becomes "Complex mutants are coupled to simple mutants in such a way that a test data set that detects all simple mutants in a program will also detect a large percentage of the complex mutants" [Offutt92]. As a result, the mutants used in traditional Mutation Testing are limited to simple mutants only.

The Process of Mutation Analysis

The traditional process of mutation analysis is illustrated in the figure below. In mutation analysis, from a program p, a set of faulty programs p' called mutants, is generated by a few single syntactic changes into the original program p. A transformation rule that generates a mutant from the original program is known as a mutation operator. In the literature of Mutation Testing, mutation operators are also known as mutant operators, mutagenic operators, mutagens and mutation rules [OffuttU01]. Typical mutation operators are designed to modify variables and expressions by replacement, insertion or deletion operators.

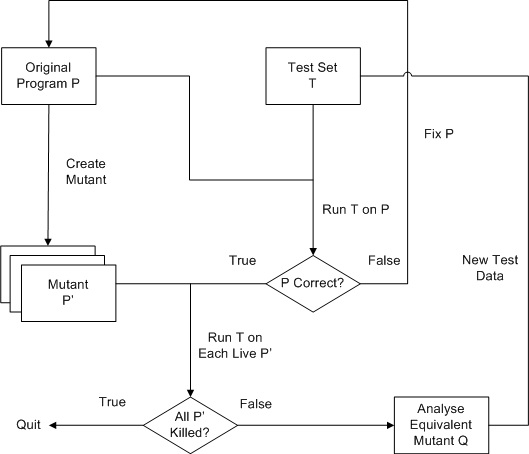
In next step, a test set T is supplied to the system. Before starting the mutation analysis, this test set needs to be successfully executed against the original program p to check its correctness for the test case. If p is incorrect, it has to be fixed before running other mutants, otherwise each mutant p' will then be run against this test set T. If the result of running p' is different from the result of running p for any test case in T, then the mutant p' is said to be "killed", otherwise it is said to have "survived".

After all test cases have been executed, there may be still a few "surviving" mutants. To improve the test set T, the program tester can provide additional test inputs to kill these surviving mutants. However, there are some mutants that can never be killed, because they always produce the same output as the original program. These mutants are called Equivalent Mutants. They are syntactically different but functionally equivalent to the original program. Automatically detecting equivalent mutants is impossible [BuddA82,OffuttP97], because the problem would involve detecting equivalence.

Mutation Testing concludes with an adequacy score, known as the Mutation Score, which indicates the quality of the input test set. The mutation score (MS) is the ratio of the number of killed mutants over the total number of non-equivalent mutants. The goal of mutation analysis is to raise the mutation score to 1, indicating the test set T is sufficient to detect all the faults denoted by the mutants.

The Problems of Mutation Analysis

Although Mutation Testing is able to effectively assess the quality of a test set, it still suffers from a number of problems. One problem that prevents Mutation Testing from becoming a practical testing technique is the high computational cost of executing the enormous number of mutants against a test set. The other problems are related to the amount of human effort involved in using Mutation Testing , for example, the human oracle problem and the equivalent mutant problem.

The human oracle problem refers to the process of checking the original program's output with each test case. Strictly speaking this is not a problem unique to Mutation Testing. In all forms of testing, once a of set inputs has been arrived at, there remains the problem of checking output. However, mutating testing is effective precisely because it is demanding and this can lead to an increase in the number of test cases, thereby increasing oracle cost. This oracle cost is often the most expensive part of the overall test activity. Also, because of the undecidability of mutant equivalence, the detection of equivalent mutants often involves additional human effort.